Pues que si no piensa que hay reversión, cuando Azvalor estaba a 50 su VL y había caído un 60%, ¿no pensaba que eso volvería a la normalidad?
Lo digo por esto que comentó.
Doy por hecho que en gestión activa, pensaba en la reversión a la media, porque si no fuera así, estaría asumiendo, cuando AZ cayó, que no iba a recuperar.
Personalmente y cuando Cobas estuvo en el -50% no pensaba en una reversión a la media sino en que dada la filosofía de inversión y el tipo de activos en los que estaban invertidos, era mas probable que eso recuperara valor que otros estilos o tipos de activo.
Pero no, no creía ni antes ni ahira que eso deba pasar como compensación estadística a nada. Esto no es como tirar una moneda que si la tira tres veces y sale las tres cara, sabe ud. que seguro que si sigue un número suficiente de veces el número de caras y cruces se acercarán al 50%. Esto no funciona así.
Es mas sencillo que todo eso . Simplemente confié en los Gestores y no pensé en absoluto en la reversión. Tan sólo " Compré " su versión y estrategia y en que, en el futuro , sus inversiones iban a " Cristalizar " como así ha sido hasta ahora ,claro . Hasta hace pocos años confundía Volatilidad con Riesgo . Por supuesto que no adiviné que subiría un 400% . En mi cartera , poseo fondos que, en un momento dado , pierden , empatan o ganan pero, en ningún caso , me planteo cambios en función de ello . A mi me sirve , poco mas puedo decirle . Cada cual debe sentirse cómodo con su estrategia y , en Gestion Activa , jamas venderé o traspasaré un fondo ( Salvo que pierda la confianza en ellos ) y , ni a 50 me sucedió con ellos . Vamos que si un día liquido un Fondo , nunca será en mínimos …
Buena recopilación de opiniones. De personas relevantes, sin duda, pero son opiniones. No hay demostraciones.
Mmmm esto hace también un porrón que no lo miro y es verdad que es un concepto escurridizo, pero el principio de reversión a la media afirma una cosa muy concreta. Dice lo que dice; y lo que no dice, no lo dice.
El principio de reversión a la media dice que cuando la correlación de 2 variables no es perfecta, que es una forma de decir que existe cierta aleatoriedad, un resultado que no se conforme a la media irá seguido por uno que esté más cerca de la misma. No dice nada de que todas las medias tengan que ser iguales.
Un ejemplo que estoy 99% seguro que he puesto en el foro, pero que no encuentro. La altura media de los holandeses es 1,80m, la de los peruanos 1,60m. Tenemos a un señor holandés que mide 2m y a un señor peruano que mide 1,40.
Lo que dice la reversión a la media es que la altura del hijo del señor holandés es más probable que esté más cerca de 1,80m que de 2m y que la altura del hijo del señor peruano más cerca de 1,60m que de 1,40. En ningún caso dice que nos quepa esperar que los 2 niños sean igual de altos.
Volviendo a Azvalor, ciertamente la han sacado del estadio este año. ¿Qué nos cabe esperar? que el los resultados del próximo año estén más cerca de la media.
¿Que el principio de reversión a la media sea una verdad matemática significa que a largo plazo Azvalor no puede hacerlo mejor que el mercado/otros? No. Azvalor puede hacerlo mejor que el mercado. Si no lo hace no tiene nada que ver con el concepto de reversión a la media.
¿Que hayan sido los primeros este año significa que al año que vienen van a ser los últimos? Hell no.
Releyéndome no tengo claro que no me haya columpiado, pero así se queda 
Recuerdo que el libro de la suerte de Maubosin, o como se escriba, trataba el tema razonablemente bien:
Saludos 
¿Esta afirmación la hace porque usted tiene conocimientos sobre biología o porque es la intuición que usted tiene?
Lo digo porque me ha sorprendido mucho. Yo, intuitivamente, ya que no tengo conocimientos de biología, diría que una persona que mide dos metros, independientemente de su raza, etnia…, debería tener hijos cercanos a los dos metros. Por supuesto, generalizando mucho, ya que influyen muchos otros factores como su pareja…
Para quien quiera profundizar le recomendaría , a parte del citado por @Helm , el libro Contra los Dioses: La extraordinaria historia del riesgo - Peter L. Bernstein
Uno de los problemas es que podemos coger unas frases de Bernstein, Bogle o Shiller, y sacándolas de contexto, interpretar lo que ellos interpretan como reversión a la media, con un significado notablemente distinto. Ojo que parte de los errores de inversión vienen de malinterpretar conceptos que suelen tener más miga de lo que puede parecer en primera instancia.
En el libro señalado, por ejemplo, Peter Bernstein señala que la reversión a la media puede tardar más tiempo del que se cree en producirse, se puede producir a unos niveles distintos de los que uno toma como referencia e incluso puede haber algún tipo de disrupción que invalide esa reversión a la media.
Por ejemplo, lejos de lo que se cree, la reversión a la media de la renta variable a una rentabilidad promedio del 8-9% tendría poco sentido esperar que se produjera en un escenario tipo la primera mitad del siglo pasado y, tampoco era la reversión a la media esperada hace 300 o 400 años donde no había ni las instituciones ni las leyes adecuadas para poder implementar como hoy dicho tipo de inversión.
Por poner otro ejemplo curioso, en la gran depresión, el presidente americano de cuando empezó, Hoover, comentó en sus inicios, que ya faltaba poco para que la situación se diera la vuelta y que el mercado, sin hacer nada, lo arreglaría todo rápidamente sin necesidad de hacer nada o casi nada. Luego resultó que la cosa se alargó durante más de 5 años desde que hizo semejante comentario y empeoró notablemente antes de la mejora que esperaba.
Saludos cordiales.
A mí me da la impresión de que la reversión a la media es un fenómeno que se observa cuando el azar tiene una fuerte componente. A veces de hacerlo las cosas mejor ya veces peor que los demás. No sé si nadie ha conseguido hacerlas siempre o casi siempre bien: ¿Buffet, Soros, Kostolany…? Ni si ha sido así ha sido porque han tenido mucho más suerte que los demás.
Lo que también se ve son fondos que desaparecen.
La marca de caer en el mismo color en forma consecutiva se logró 16 años antes en Estados Unidos, al caer la bola 32 veces consecutivas en el rojo. Por su parte, el negro “solo” ha salido en 26 ocasiones seguidas y eso fue hace más de 100 años.
Conoce los récords de la ruleta
Aqui una conferencia de J Bogle en el MIT en 1998 sobre Fondos de Inversion y Reversion a la Media:
Interesantes reflexiones las que se han volcado últimamente.
A mi me sorprende lo convencidos que están algunos foreros sobre sus decisiones.
Yo dudo todo el tiempo sobre mi cartera. Bueno no soy una persona que viva en la incertidumbre pero no tengo la más remota idea de que mis fondos lo vayan a hacer bien de aquí hasta el fin de mis días.
Habrán crisis, cambios de regulaciones, escisiones de gestores… Tantas variables y tantas otras que desconocemos…
Es por ello importante el leer, informarse, corroborar datos, etc. Y el que todos Uds hagan de abogado de Diablo no hace más que ayudar a todos nosotros antes de tomar una decisión.
Así lo veo yo.
Conociendo un poco a Bogle diría que su objetivo con estos comentarios es más dudar de la habilidad como motivo que produce la rentabilidad de los fondos activos respecto al índice, que incidir en que sea buena idea seguir algún tipo de estrategia seleccionando fondos de gestión activos que lo han hecho peor que la media.
Recuerdo bastante bien que muestra sus dudas que algún tipo de gestión con factores aporte por ejemplo un plus de rentabilidad (tipo value versus growth u otros factores) a un inversor particular porque puede pasar perfectamente que en el plazo del inversor, no se manifieste dicho plus incluso en el caso que pudiera existir, además de la sabida dificultad del inversor para aguantar periodos largos de peor rentabilidad relativa respecto a una opción más general.
Otra cosa donde incide mucho Bogle es en la incapacidad de generar valor rotando fondos activos y es especialmente crítico con los fondos de fondos, no sólo con la capa adicional de comisiones que suelen llevar sino también por su tendencia a moverse a destiempo. No parece muy convencido que pudieran aportar valor rotando de fondos más de moda a otros más castigados incluso aunque exista reversión a la media.
Apenas miro los mercados. Tengo una cartera de fondos que apenas toco.
Tengo la impresión de que los índices de las empresas europeas últimamente lo están haciendo peor que los índices de las empresas estadounidenses.
¿Eso implica que necesariamente que, por la reversión a la media, dentro de un tiempo las empresas europeas lo van a hacer mejor que las empresas estadounidenses?
¿No podría darse el caso de que las empresas europeas se vayan quedando atrás y llegue un momento en el que ya no puedan alcanzar los rendimientos de las empresas estadounidenses durante muchos muchos años?
No recuerdo en qué libro leí un caso acerca de la reversión a la media en las maniobras de los pilotos de combate que creo que puede tener cierta analogía con la inversión.
El tema era que estaban estudiando el efecto de la recompensa/castigo tras cada día de ejercicios. A los pilotos que lo habían hecho mejor un día los premiaban y a los que lo habían hecho peor los castigaban. Al día siguiente veían que los pilotos que lo habían hecho mejor el día anterior tendían a hacerlo peor y viceversa. A priori esto podía deberse a que el castigo funcionaba y la recompensa no, pero se dieron cuenta que no era más que el efecto de la reversión a la media.
El performance de un piloto viene determinado por su habilidad (contrastada por las pruebas que han tenido que pasar previamente) y por la suerte que haya tenido ese día. Y es este último término el que está sujeto a la reversión a la media .
Yo veo el caso de los gestores de forma análoga. Como decía @Buso, cualquier resultado debido al azar estará sujeto a la reversión a la media. Y ahí está el quid de la cuestión: ¿Cuánto de azar y cuánto de habilidad tiene el resultado de una inversión?
Si concluimos que la parte de azar es relevante podemos esperar que se produzca reversión a la media pero en ese caso, ¿qué sentido tendría confiar en un gestor?
Me está sonando uno de Michael Lewis, se trata de Deshaciendo errores: Kahneman, Tversky y la amistad que nos enseño como funciona la mente. En él se explora la amistad entre Kahneman y Tversky y su arranque en el ejército israelí hasta obtener el premio nobel.
Hola, vaya por delante que no me siento cómodo hablando de cosas que no domino razonablemente. Aunque el insight original, si no recuerdo mal, viene de la genética, de un tal Galton o Dalton, que al parecer era primo de Darwin, no hace falta saber de genética, o finanzas o de nada: es un principio/teorema/lo-que-sea de mates/estadística. Lo único que necesitamos es que 2 variables o 2 medidas de una variable no exhiban correlación perfecta. En el caso de la altura, si un padre mide 2m y su hijo 2m y el nieto 2m, podemos concluir que la altura está 100% determinada por la genética del progenitor. Para cualquier otro caso tenemos que admitir que, la genética cuenta en parte, y luego hay otras cosas que desconocemos que influyen, a esas cosas las empaquetamos juntas y las llamamos aleatoriedad, o buena/mala suerte. Lo que dice la regresión a la media es que a una medida que no sea la media, en general; o a una medida extrema lejos de la media, en particular; es más probable que le siga una medida más cercana a la media. Seguro que hay una demostración formal que por supuesto desconozco.
///
De todas formas ojo con generalizar resultados/teoremas que no sabemos que supuestos (assumptions) llevan implícitos. Porque, por ejemplo, anoche, un instante infinitesimal después de decir que no sabía si me había columpiado con lo que había dicho, se asomó mi señora por detrás y me apuñaló con un but you know that’s only true for stationary processes, don’t you? So go figure!
////
Indeed, la historia esa es de Kahneman cuando empezó su carrera en ejército israelí. Es un ejemplo de lo que esta gente llama el espejismo de la causa y efecto. Lo cuenta también en Thinking Fast & Slow.
Yo me cuelo entre la vorágine value para colar un “yo he venido a hablar de mi libro”…
Cuando se habla de regresión a la media, hay diferentes contextos. En estadística y teoría de la probabilidad están modelizados y tienen su forma de tratarse, aunque yo no sepa mucho tampoco al respecto sé lo suficiente para saber que existen y he utilizado de manera básica algunos de los teoremas donde se habla de las premisas y las demostraciones.
Este concepto da lugar a múltiples falacias, una de las más conocidas es la falacia del apostador, donde el ejemplo típico es que si al apostar comienzan a aparecer X caras o cruces seguidas, se cree que existe una fuerza invisible que hace que en el siguiente resultado sea más probable que aparezca el lado contrario, cuando una vez ya ocurridos los eventos la probabilidad es la misma que en el primer lanzamiento, un 50% ya que son eventos aleatorios independientes.
En resumen, la regresión a la media pura, estadísticamente hablando se trata en el conjunto de teoremas englobados bajo la ley de los grandes números, estos teoremas si se cumplen sus premisas, implican que con una gran cantidad de ensayos el resultado esperado se acerca a la media esperada de la distribución subyacente, eso también implica que una muestra lo suficientemente grande de una población nos servirá también para hacer ciertas estimaciones sobre su distribución futura ( siempre y cuando sepamos que las muestras pertenecen todas a una misma distribución ). Las premisas sin embargo para que esto se cumplan son importantes, si no, no podemos aplicar estas deducciones, por ejemplo que deben ser una sucesión infinita de variables aleatorias independientes con valor esperado/varianza determinada o idénticamente distribuidas. Incluso cuando se cumplen las premisas el número de ensayos debe ser muy grande y dependiendo de si usamos la ley fuerte o débil de los grandes números debemos usar términos como “casi con seguridad” o “seguramente” más que hablar de certezas. .
Por otro lado, en finanzas se utiliza mucho el concepto de regresión a la media pero que en las series de tiempo en estadística en realidad se denomina “seasonality” o estacionalidad, que son los ciclos que sufren los negocios en sus retornos dependiendo de las variables macroeconómicas e idiosincrasias de sus negocios ( por ejemplo si se ven más o menos beneficiadas en un entorno u otro ) .
Un caso típico de esto que ya he comentado es el lanzamiento de una moneda suponiendo que siempre se lanza en condiciones ideales o la de uno o dos dados. Aquí por ejemplo tenemos el histograma de frecuencia del lanzamiento de dos dados y la suma del resultado:
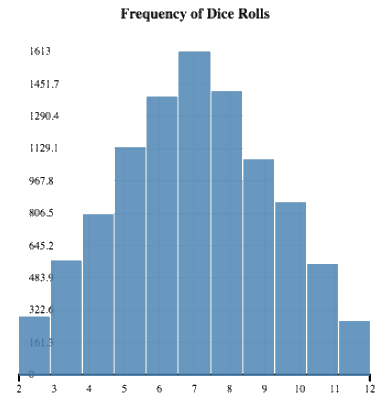
Como sabemos que los resultados son aleatorios e independientes y tienen una distribución subyacente que no cambia ( no trucamos el dado a mitad de tiradas ) podemos aplicar la ley de los grandes números y además podemos afirmar que es un sistema ergódico, esto es, que si hiciéramos tiradas en paralelo de millones de dados la media de todos esos sistemas convergería en la misma media.
Sin embargo, esto no debe extrapolarse a un histograma de resultados del SP500:
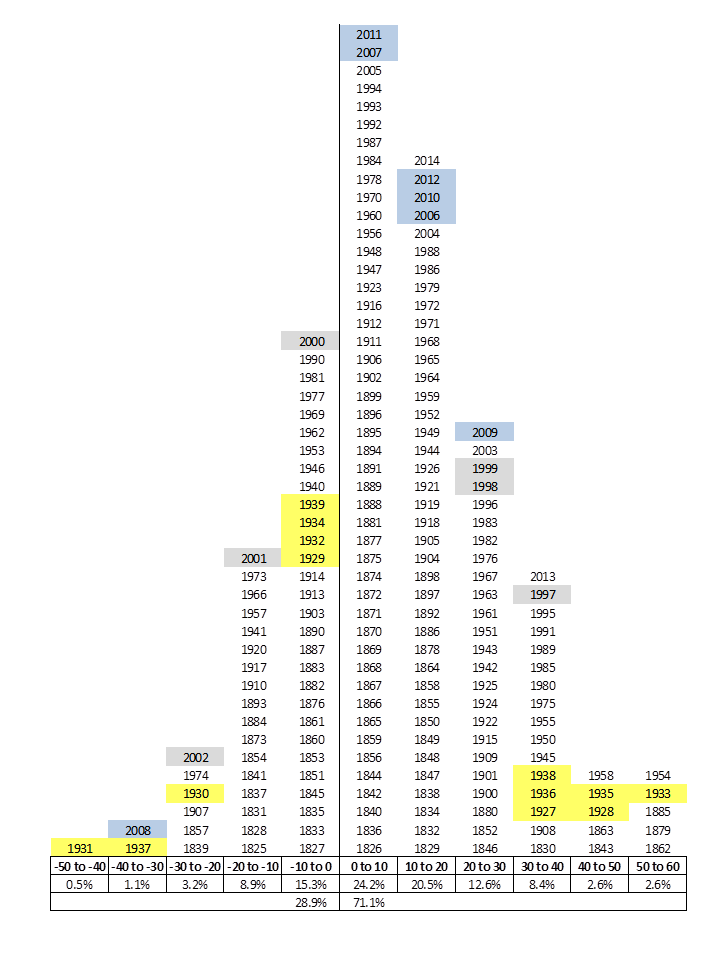
Aquí no se cumplen múltiples premisas de la ley de los grandes números, no todos estos resultados corresponden a la misma distribución subyacente, esto es, cada época tenía sus variables externas que influían en este resultado que desconocemos, tenemos pocas tiradas y además podemos afirmar que depende del camino inversor que hayamos escogido, el año, la cantidad etc incluso aunque tuviéramos infinitas tiradas, sería un sistema no ergódico donde si tuviéramos miles de inversores en paralelo no nos garantizaría que convergieran a la misma media.
Por eso siempre se hace hincapié como comentaban @Helm y @agenjordi a que nada garantiza que en nuestra “tirada inversora” las medias se cumplan y de ahí la racionalidad de hacer market timing o usar estrategias defensivas alejadas del inversor ideal centrado solo en busca del ratio óptimo entre volatilidad y retornos de la frontera eficiente que describía Markowitz o el CAPM.
Aplicar la estadística pura a este tipo de resultados para prever el futuro en nuestra vida inversora no nos sirve de mucho, lo que sí nos sirve es para entender parte de la historia del activo, y digo parte por que la otra parte la debemos complementar con los drivers de generación de valor del activo y en qué sustentan para vigilar si siguen siendo válidos en el futuro y entender cuando el activo se aleja de los mismos.
Entonces y en resumen, en mi opinión, en RV se suele usar mucho el concepto de regresión a la media de manera mucho más informal ( por que realmente no podría aplicarse ) cuando el valor actual se aleja de los fundamentales del activo bajo situaciones macro similares etc, pero hay también hay quien lo utiliza mirando el precio histórico y apuesta a variables de demanda y oferta, etc. En esos casos el concepto de reversión a la media me parece que está mal utilizado ( desde un punto de vista puramente estadístico ) y que se está apostando en parte a la estacionalidad y otras cuestiones.
Bueno he hecho un batiburrillo mezclando algo los temas, pero eso me pasa por no “haber estudiao” como me diría @Helm
Para mí la reversión a la media sólo es esta:
Junto con los beneficios normalizados del ciclo, que está ligado a esta gráfica también.
Y claro, con esto hay matices como que haya un cambio estructural en el sector y compañías o índices que ya jamás vuelvan a cotizar a su múltiplo medio.
Se habla mucho de Azvalor este año, pero ojo con Turquía @MAA que lleva ya un doblete 
Turquía está sufriendo una crisis económica tremenda y su bolsa se dispara. A veces funciona como refugio contra la inflación como ya han advertido desde Cobas y Azvalor y creo haber leído a Kostolany. Así mismo como refugio contra una crisis. Como consecuencia el mercado puede subir y mucho. Creo que se pueden tener esperanzas que no nos vaya mal en 2023 cuando según parece tendremos una crisis económica en Occidente.
