La ansiedad financiera que crece con las deudas: "Todo era un caos cuando empezamos a pedir minicréditos, tarjetas revolving..." | Dinero e inversión cosas que pasan cuando vas de microcrédito en microcrédito (yo he conocido a varios). Para leer libremente, aquí https://archive.ph/c4pnC
3 Me gusta
¿Le suena el concepto anatocismo?
4 Me gusta
Pues no, una cosa más que hemos aprendido.
Es importante saber a quién escuchar y también a quién no escuchar.
24 Me gusta
Este post que Vd. pone es un ataque indiscriminado a todos nuestros queridos economistas austriacos, conspiranoicos y patreones de este foro. ¿Qué será lo siguiente, decir que nos hagamos pedristas?
No tiro la piedra sin esconder la mano… ¿de qué vamos a hablar aquí si no podemos?
- mostrar gráficos cotizados en oro, en bitcoins o en cualquier cosa que no sirva para nada
- ignorar los dividendos ¡EN ESTE FORO!
- comparar la velocidad con el tocino
- introducir nuestros sesgos políticos en nuestros análisis objetivos
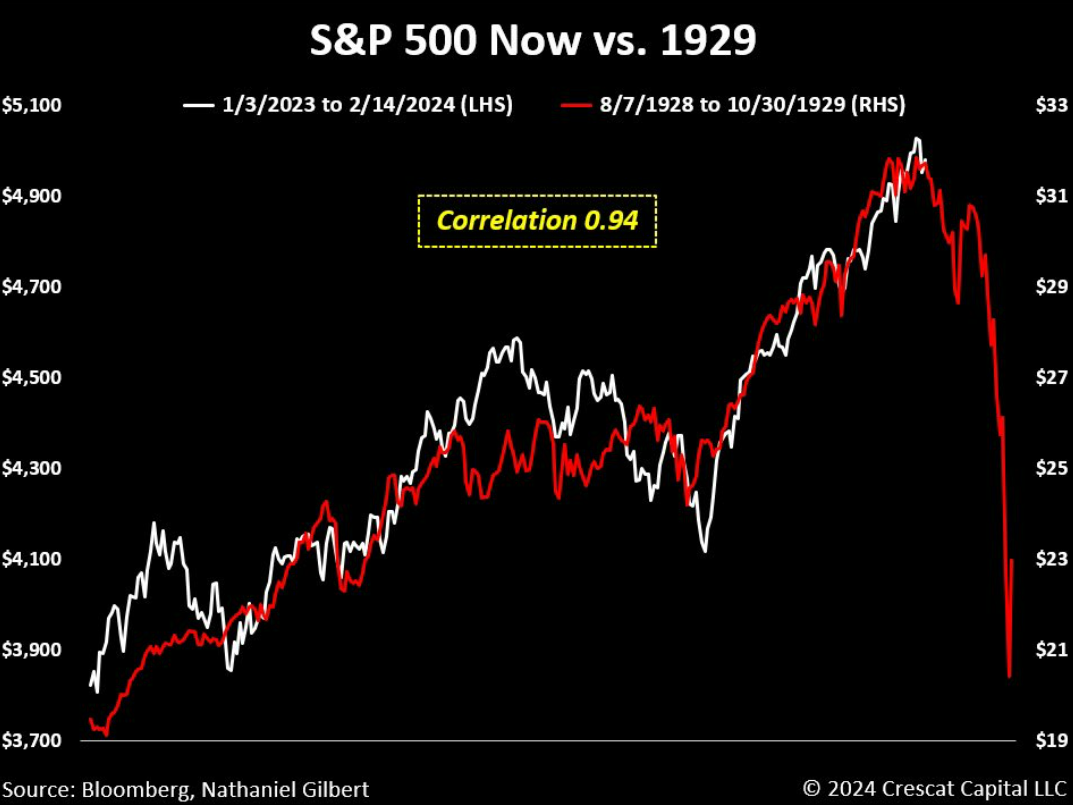
- poner gráficos sin incluir el crash del 29 para ver que en 5 años estaremos ahí otra vez
- hablar del colapso financiero que está a la vuelta de la esquina
- utilizar 1 ó 2 hitos gráficos para predecir el futuro
- criticar a las monedas fiduciaras y a los bancos centrales
¿De qué quiere Vd. que hablemos, ínclito @Cygnus? ¿qué se cree que es esto, comprar y mantener? Dese por apercibido
23 Me gusta
Es significativo que algunos vean gran correlación en este tipo de gráficos.
Mi sensación es que sus conocimientos estadísticos son bastante pobres por no decir nulos.
Mirando muchos comentarios en redes de inversión parece como si la estadística fuera una disciplina más parecida a la alquimia que a cualquier cosa con unos mínimos de base matemática.
19 Me gusta
¿Es que insinúa que la correlación no está? Y AQUÍ QUÉ ¿TAMPOCO ESTÁ?
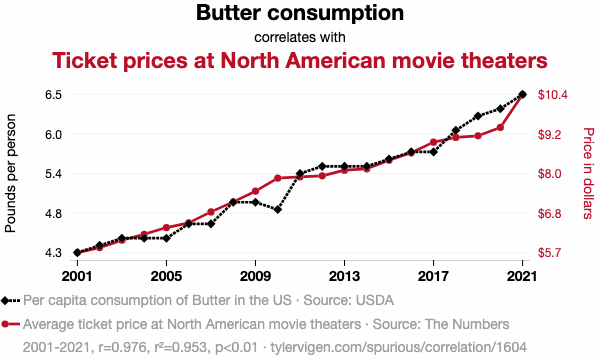
(¿se estrenó El Último Tango en París en 2001?)
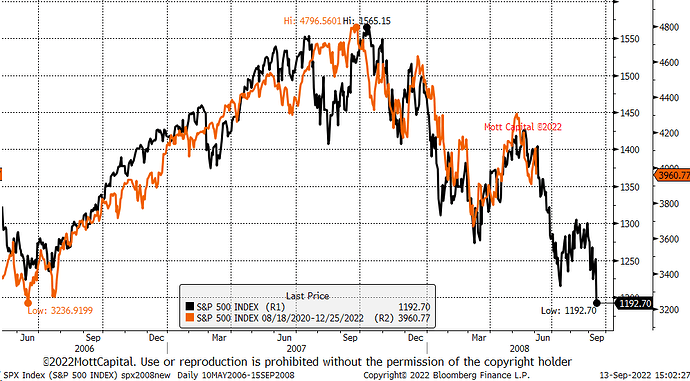
¿y qué me dice esta, tampoco ve la correlación?
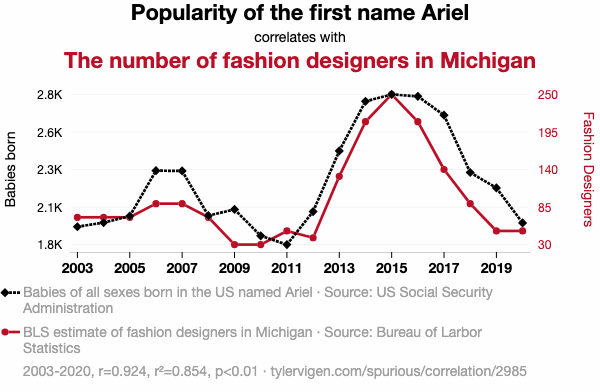
Para que acabe con su descreimiento le dejo todo un escapate
21 Me gusta
Buenos días:
es absurdo y una pérdida de tiempo andar siguiendo los VL´s día a día; pero todavía lo es más, a mi parecer, buscar correlaciones entre el tocino y la velocidad.
Cuando más tranquilamente aporté al SP&500 es en el 2022 cuando los “expertos en curvas” presagiaban su derrumbe (por correlación con el 2008):
Un saludo.
6 Me gusta
13 Me gusta
6 Me gusta
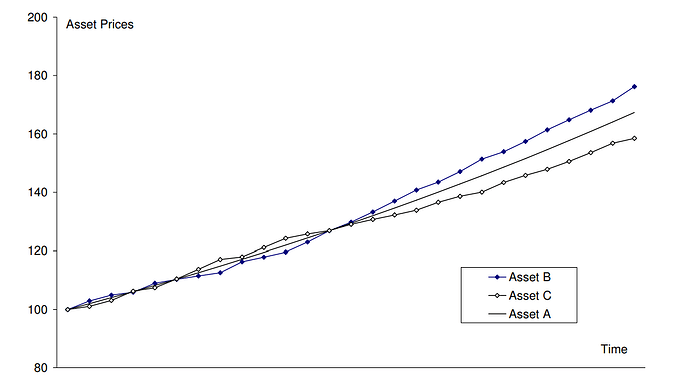
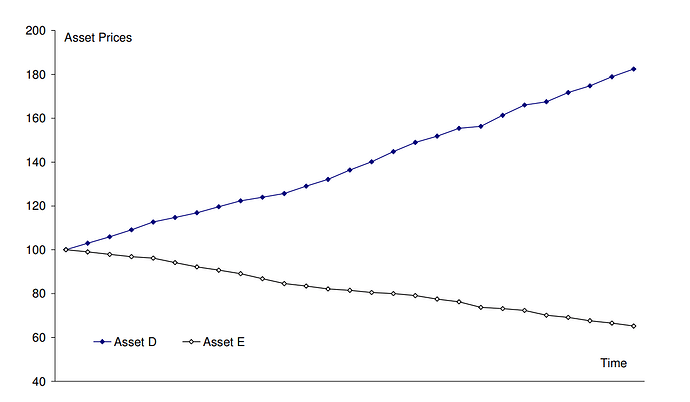
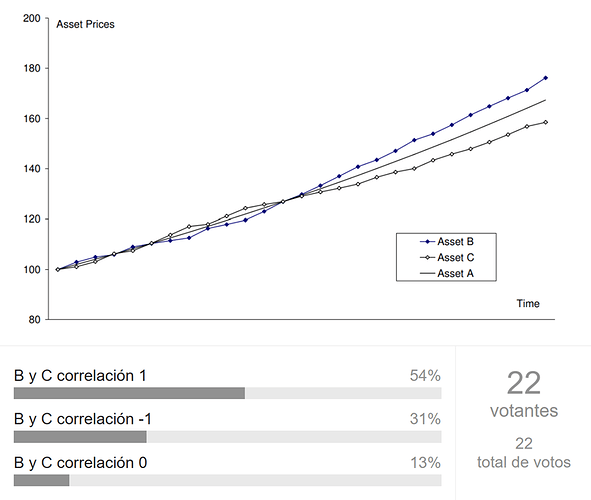
Les dejo con un pequeña encuesta a ver qué opinan de la relación entre los activos de estos gráficos, voten sin miedo que es anónima :
- B y C correlación 1
- B y C correlación -1
- B y C correlación 0
0
votantes
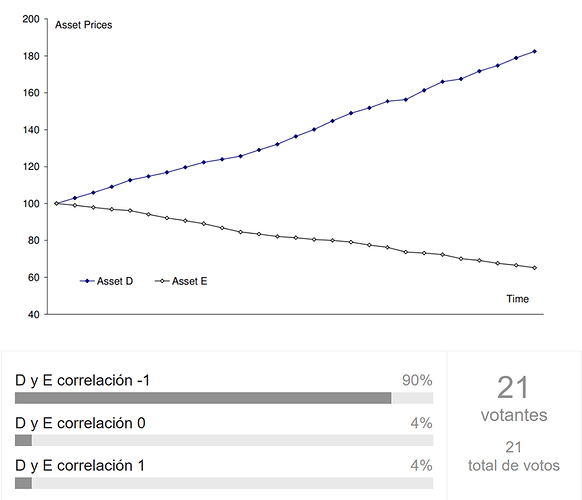
- D y E correlación 1
- D y E correlación -1
- D y E correlación 0
0
votantes
6 Me gusta
Es Vd. un tahúr de los datos. Se pueden hacer correlaciones verdaderamente curiosas, depende de los números, pero el punto no es ese!!!
4 Me gusta
Mi post no es una crítica al suyo, es algo que creo que beneficiará a la comunidad y ya que soy un vago para escribir artículos lo he hilado con el suyo.
Fíjese que no me he metido con el uso incorrecto de Pearson que se hace en esos gráficos y estoy hablando de finanzas 
9 Me gusta
Aquí les dejo un hilo que he escrito como refuerzo de lo aprendido, y porque me ha parecido interesante compartirlo sobre las corridas (aquí sí lo digo así, que se que son Vds. más adultos que la media) bancarias x.com
5 Me gusta
Ya han pasado un par de días desde mi post, así que voy a dar la solución a la encuesta sobre correlaciones.
En primero de los gráficos, las respuestas han sido estas:
La gráfica 1 ilustra una trayectoria simulada para los precios de los tres activos. Los activos B y los precios de C parecen oscilar alrededor del activo A. El componente de tendencia domina en el largo plazo, ya que las variaciones estocásticas alrededor de la tendencia tienden a revertirse en el tiempo debido a su media cero. La mayoría de los inversores que observen esta figura concluirían que los activos B y C están casi perfectamente correlacionados positivamente, y sí, están perfectamente correlacionados, pero negativamente porque sus desviaciones de la media son idénticas, pero de signos opuestos.
En el segundo de los gráficos, las respuestas han sido estas:
La gráfica 2 ilustra una trayectoria simulada para los precios de los dos activos. Los activos D y E parecen oscilar en torno a dos tendencias muy diferentes. Estos componentes de tendencia dominan en el largo plazo, ya que las variaciones alrededor de la tendencia tienden a revertir a la media con el tiempo. La mayoría de los inversores que observen esta gráfica concluirían que los activos D y E son de una correlación negativa casi perfecta. Error de nuevo, de hecho, están perfectamente correlacionados positivamente, porque las desviaciones desde sus respectivas medias son idénticas y el signo del componente de tendencia no importa en el cálculo del coeficiente de correlación .
Explicación más técnica para los que les interese:
En diversos textos de economistas o profesionales de inversión se pueden leer definiciones de este tipo:
“Si la correlación entre dos activos es +1, se dice que están perfectamente correlacionados. Sus retornos siempre se mueven en el misma dirección al mismo tiempo y en las mismas cantidades. Si la correlación es -1, los activos se dice que están correlacionados negativamente. Sus retornos siempre se mueven en direcciones opuestas, en cantidades exactamente opuestas"
Esto es un error y es lo que ha causado bastante confusión entre muchos inversores, ya que la correlación se calcula desde la desviación de la media de cada conjunto de datos, por lo que no nos indica nada de la tendencia que tiene ese conjunto de datos. Lo podemos observar en la fórmula del cálculo. Ambas correlaciones están calculadas con el método Pearson. El método Pearson se define con esta ecuación:
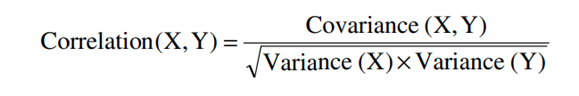
Que es equivalente a esta otra:
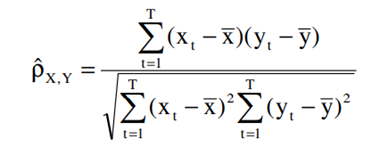
Dónde estos símbolos representan la media de ambos conjuntos de datos:
Por lo tanto podemos observar que esta fórmula realmente no tiene en cuenta si el precio del activo sube o baja ( la tendencia ) , solamente el cambio respecto a su media. Esto es peligroso por que a la hora de calcular o no la correlación con un activo que metemos en cartera podemos estar ignorando las tendencias del activo. Y es que esta fórmula también nos revela más información, al usar el cambio frente a su media, lo que nos indica también es que está asumiendo cierta distribución en los datos.
La fórmula de Pearson no sirve para:
-
Conjuntos de datos que no cumplan con una distribución normal, por ejemplo el precio de muchos activos tiene una distribución no uniforme con “colas anchas” ( Kurtosis más o menos altas )
-
Es muy vulnerable a outliers, por que influyen mucho en su media. No sirve para reflejar fielmente eventos como un crash bursátil, esto es, no refleja las correlaciones entre las colas de los activos ( cuando hay drawdowns o subidas muy pronunciadas ).
-
También es floja capturando correlaciones que no sean lineales. Una relación lineal se puede definir como la ecuación de una línea recta, donde existe un componente que avanza en proporción al otro. En una relación no lineal, o monotónica puede las cambian pero no tienen por qué hacerlo en la misma proporción, por ejemplo en una relación curva.
El resumen, aunque no hayan entendido todo lo anterior, la idea que quiero transmitir es que sin entrar en el detalle técnico de como está calculado un parámetro no lo utilicen para sus decisiones de inversión. Y por supuesto, cuando les muestren un gráfico con dos líneas que van en la misma dirección no asuman correlación por que simplemente puede ser que compartan la misma tendencia.
27 Me gusta
Saludos cordiales, @AlanTuring.
¿De dónde ha sacado estos ejemplos? Porque en sus gráficas hay dos muestras de datos con dos variables, es decir, cuatro series de datos respecto de un parámetro t: {(x¹(t), y¹(t)) / t € T} y {(x¹²(t), y²(t)) / t € T }. Sin embargo, el coeficiente de correlación de Pearson se calcula para una sola muestra de datos bidimensional.
Si el conjunto de parámetros T es el mismo para ambas muestras podríamos reducir el número de series a dos si representamos yⁱ = xⁱ(t) con i = 1, 2 y correlacionar el par de series {(y¹, y²)}.
1 me gusta
Es solo una muestra de datos pero la muestra es de dos variables. No le entiendo o está liándose.
1 me gusta
Que cada muestra es de dos variables y presenta dos muestras. ¿Cómo calcula r que solo admite dos series de datos {(xᵢ, yᵢ)} en su cálculo si tenemos cuatro?
Proponga ejemplos con datos e intente mostrar cómo calcularlo.
La evolución de cada activo está representado por una muestra bidimensional precio / tiempo.
1 me gusta
Yo creo que está claro que hay dos variables de precio y una de tiempo que es compartida que une ambos, por lo tanto la tabla de datos la componen el precio de cada activo, dos precios, dos variables.
Yo le pediría que antes de contaminar el hilo con preguntas de este tipo primero le de una pensada al tema.
Ponemos un ejemplo y calculemos la correlación entre las series {(y¹, y²)}. En el primer caso se ajustarán a una recta y = +ax + b; en el segundo con y = –x.
Nota: y = ax + b representa lo mismo que u = αv + β.
Yo no creo que sea una contaminación. Creo que es la interpretación correcta argumentada.
2 Me gusta