Originalmente publicado en: Del corral al parqué: Probabilidad e Incertidumbre – Todo suma
Algo tienen las aves de corral para haberse convertido en parte imprescindible del recetario filosófico. Aunque el tema de hoy no es el manido “¿qué fue antes, el huevo o la gallina?” Si no lo que influenció a Nassin Nicholas Taleb para convertir el ejemplo del pavo antes de Acción de Gracias en un elemento más de la cultura popular: La gallina de Russell.
Bertrand Russell, el que para muchos es el filósofo anglosajón más influyente del siglo XX, se esforzó por eliminar de la filosofía las suposiciones que en su opinión resultaban absurdas e incoherentes. Esto le acabaría otorgando no solo un espacio entre los grandes filósofos de la historia, sino también un hueco en el corazoncito de muchos amantes de la Filosofía y, sobre todo, la Ciencia, que rehusaban seguir los complejos derroteros por los que se había ido la primera y que amenazaba con relativizarlo todo. Fue un puente crucial entre la filosofía tradicional y las corrientes analíticas porque transformó el enfoque filosófico al priorizar el rigor lógico y la claridad conceptual sobre las especulaciones metafísicas abstractas que caracterizaban a muchas de las escuelas previas.
Es muy probable que recurra a su figura en más ocasiones porque sus contribuciones en lógica matemática, especialmente a través de obras como Principia Mathematica (1910-1913) (en coautoría con Alfred North Whitehead), cimentaron los fundamentos de la lógica moderna, influyendo profundamente en áreas como la informática y la teoría de conjuntos.
Russell abordó una amplia variedad de temas filosóficos, pero vuelvo a su célebre ejemplo de la gallina (o pollo), que ya mencioné anteriormente para ilustrar las limitaciones del razonamiento inductivo. Por si se perdió ese capítulo, según este razonamiento, la gallina que recibe comida todos los días por parte del granjero acaba esperando que la rutina continúe indefinidamente, y asocia la presencia del granjero con alimento. Sin embargo, su visión inductiva del mundo no contempla que un día cualquiera esa misma presencia traerá consigo la muerte, una conclusión completamente inesperada dentro del marco de sus experiencias previas.
En este contexto, la probabilidad, una disciplina que encuentra su hogar entre la matemática y la estadística surge como una herramienta fundamental para evaluar la incertidumbre y tratar de cuantificar el riesgo en escenarios donde la inducción, por sí sola, no puede garantizar certeza. Pese a también depender de patrones pasados, permite modelar escenarios futuros con distintos grados de confianza. A través de su estudio, la humanidad ha desarrollado conceptos muy importantes y útiles que ayudan a medir la frecuencia esperada de ciertos eventos, salvando muchas vidas por el camino y ayudando al progreso.
Pese a que su estructura matemática proporciona una base más sólida para tomar decisiones en un mundo incierto, la probabilidad tampoco es infalible ante «cisnes negros». Porque ¿qué probabilidad puede tener algo que nunca se ha observado?
Midiendo lo incierto:
Decía Russel que la fuerza de las certezas aumenta en función de la repetición de casos observados, y he aquí el primer problema: ¿quién define cuales son los distintos casos posibles? Parece que las teorías y la experiencia previa son responsables, y aquí empieza a oler a más problemas.
En probabilidad se define el concepto de espacio muestral como el conjunto de todos los resultados posibles de un experimento o fenómeno aleatorio. Por ejemplo, al lanzar un dado de seis caras, el espacio muestral está compuesto por los números {1,2,3,4,5,6}. La probabilidad de cada evento individual dentro de este espacio puede variar según las condiciones y la información disponible, lo que conecta directamente con nuestro filósofo de día: cuantas más veces observemos un evento dentro del espacio muestral, más fuertes serán nuestras conclusiones probabilísticas, aunque nunca podamos alcanzar una certeza absoluta.
El espacio muestral puede estar incompleto, como por ejemplo en el lanzamiento de una moneda cuyo espacio muestral muchos definirían como {cara, cruz}, pero ¿es realmente imposible que caiga de canto? Es algo ciertamente improbable, pero si se lanzase sobre un terreno embarrado, dónde la moneda puede quedarse clavada, quizás se pudiese observar por primera vez tal evento «imposible». Aquí se corre el riesgo de pensar que lo que se ve es todo lo que hay, que dirían Daniel Kahneman y Amos Tversky, pero no suele ser una premisa válida para explicar cómo funciona la realidad.
Para intentar que el espacio muestral cubra el máximo número de opciones y las conclusiones sean lo más representativas posibles, es crucial considerar el tamaño muestral en los análisis, algo que también le recomendaría el propio Kahneman (para que vea que aquí no solo se habla de filósofos). Este concepto determina cuántos casos se deben observar o experimentar para garantizar que las inferencias sean confiables. Por ejemplo, si solo se observa un lanzamiento de un dado y sale un «6», se podría caer en la falsa conclusión de que “6” es el único resultado posible. Sólo al ampliar el tamaño muestral hasta realizar lanzamientos infinitos se podría deducir que todos los números del 1 al 6 son igualmente probables en un dado perfecto. En la práctica, con un tamaño lo suficientemente grande se confirmaría esa tendencia, pese a no conseguir un resultado perfecto.
Calcular el tamaño muestral mínimo necesario es, por tanto, una tarea clave para unir la teoría y la práctica. No se preocupe que esto no es se va a convertir en una clase llena de cálculos (aún). Obviando las fórmulas matemáticas, es importante mencionar que los siguientes factores afectan a la hora de calcular el tamaño de la muestra.
- Variabilidad de la población: Cuanto más variabilidad, mayor tamaño de muestra será necesario para que la aparición de casos menos probables se ajuste. En el ejemplo del dado todos los casos son igualmente probables, por lo que un tamaño comedido de la muestra puede arrojar resultados cercanos a la realidad. Por el contrario, la mayor variabilidad natural entre individuos hace que se den resultados poco significativos cuando se mide el desempeño académico en escuelas de pocos alumnos, sobrerrepresentando los casos extremos.
- Nivel de confianza: Cuanta más confianza se exija, mayor tamaño será necesario. Intuitivamente, la muestra tendrá que ser más grande para obtener un nivel de certeza del 99% que del 95%.
- Margen de error: Inversamente proporcional a la precisión exigida, es decir, cuánto se permite a los resultados que se alejen de la realidad. Cuanto menor margen de error, mayor será la muestra requerida.
- Tamaño de la población: La población, o grupo de interés del que se extrae la muestra, se refiere al total de individuos, eventos o elementos que comparten la característica específica que se desea medir. En el caso de la tirada de dados podría tratarse de los cientos de dados de un determinado casino. En el ejemplo de las escuelas, la población podría ser el conjunto de los estudiantes de un país, y el tamaño medirse en millones. Cuanto más grande sea el tamaño, mayor será la muestra necesaria.
Es bastante común encontrar literatura académica reconociendo que un tamaño de muestra insuficiente ha invalidado la credibilidad de ciertos experimentos. No se trata de una cuestión de vaguería de los investigadores, en muchos casos el tamaño de la muestra necesario puede hacer que un experimento sea imposible de realizar y haya que sacrificar alguno de los factores mencionados.
Fuera del mundo académico le resultará familiar el caso de los sondeos previos a las elecciones democráticas. Como referencia, en España el famoso CIS (Centro de Investigaciones Sociológicas) suele entrevistar a 4000 personas en edad de votar, cifra calculada a partir de un nivel de confianza de 95.5% y un margen de error del 1,6% para el conjunto de la muestra. Nunca he visto al CIS predecir que habría sobres con lonchas de chorizo en su interior, pero para alegría de los noticiarios suele haber alguna cada año, por lo que parece que el espacio muestral no coincide con la realidad en su totalidad.
También habrá algún que otro ejemplo en el que el CIS no haya acertado demasiado midiendo la intención de voto. Tampoco parece un trabajo sencillo por múltiples motivos. En primer lugar podemos echar mano al concepto de reactividad psicológica —fenómeno por el cual los individuos alteran su comportamiento o conducta cuando sospechan que están siendo observados—. Además se rompe el principio básico del secreto del voto, por lo que la pregunta no se ajusta a la acción en su totalidad, la encuesta no se hace el mismo día que la votación, no se conocen los incentivos de los entrevistados, y la variabilidad de las opciones es elevada debido a las circunscripciones. De hecho se observa que el error por comunidad es mucho más alto que el teórico utilizado para calcular el tamaño.
Podría uno llegar a pensar que hasta un mono lanzando dardos acertaría más veces. Aunque el ejemplo es robado del mundo de la inversión (al que acabaremos llegando), hay un último concepto pendiente antes de saltar a nuestra parcelita: ¿Qué hay de realidad en tal afirmación?
La tasa base: cuando todo lo demás no aporta
La tasa base tiene mucho que ver con la afirmación de los monos. Para explicar el concepto partamos del siguiente ejemplo: “puede llover”. Esta afirmación es bastante vaga y, sin más información, sólo se podría suponer que la probabilidad de lluvia es de un 50%, una estimación basada puramente en la incertidumbre. La tasa base (o prevalencia base) se refiere a la probabilidad inicial de un evento antes de considerar cualquier información adicional. En el ejemplo: 0.5 (50%). Sin embargo, este número puede cambiar a medida que se obtienen más datos.
Primer ajuste: Contexto geográfico
Si quienes participan en la conversación están en Sevilla en pleno agosto, intuirían que pueden ajustar su tasa base hacia abajo. La nueva tasa base se calibrará, partiendo de la primera, en función a la evidencia histórica relevante que dice que la lluvia en esa región y época del año es extremadamente rara. Esto estrecha la creencia inicial hacia una probabilidad mucho menor, quizás cercana al 1%, que será el siguiente punto de partida.
Segundo ajuste: Un dato nuevo
El servicio meteorológico andaluz informa de la existencia de un frente de baja presión que podría traer lluvias a la región. Este nuevo dato es una evidencia que debe combinarse con la tasa base anterior para calcular la nueva referencia. Imagine que según los meteorólogos, cuando llueve hay un 50% de probabilidad de que se den estos frentes. Esto no quiere decir que la nueva tasa base sea del 50%, sino que será el resultado de ajustar el 1% original con esta nueva información. Aquí entra en juego el teorema de Bayes, y en este caso sí es conveniente navegar un ejemplo práctico para ver por qué, dado que el ser humano es bastante malo trabajando con estadísticas y probabilidades.
El teorema de Bayes define la siguiente fórmula para calcular la probabilidad actualizada de A (la lluvia del ejemplo) dado que B (frente de baja presión):
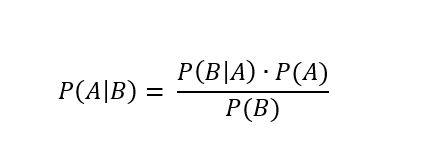
Donde:
- P(A) es la probabilidad inicial (la tasa base) de que ocurra el evento A, como la probabilidad de lluvia en Sevilla en agosto (muy baja). Para el ejemplo 0.01 (1%).
- P(B|A) es la probabilidad de observar la nueva evidencia B (frente de baja presión) dado que A es cierto (si llueve). Para el ejemplo pondré que van de la mano la mitad de las veces: 0.5 (50%).
- P(B) es la probabilidad total de observar B, independientemente de si A ocurre o no (frente de baja presión llueva o no, también improbable en Sevilla en agosto). Para el ejemplo 0.02 (2%).
- P(A|B) es la probabilidad actualizada de A (lluvia) dado que se ha observado B (frente de baja presión). Se denomina “probabilidad posterior”. Haciendo los números, la nueva tasa base es de 25%.
Puede pararse y hacer los cálculos a mano para ver dónde se ha ido el otro 25% que nos separa del número que intuitivamente esperaríamos encontrar.
Sólo encontraría un 50% si la probabilidad (tasa base) de frentes fuese exactamente la misma que la de lluvia, pero no es raro pensar que habrá ocasiones en las que haya frentes y no llueva (viento, nubes, etc.), y viceversa, llueva aunque no haya frentes. También podríamos obtener un 50% si la única causa de lluvia fuesen los frentes (P(B|A) sería 100%), pero aun así dependería de la relación entre frecuencias de cada evento.
Es posible que el ejemplo le haya creado cierto desconcierto si no está familiarizado con el tema (o si es meteorólogo y he dicho alguna barbaridad, ante la cual pido disculpas). La psicología cognitiva explica que nuestro cerebro no está feliz cuando algo resulta complejo de procesar. Para aliviar esa sensación de esfuerzo puede tomar algún dulce o seguir leyendo, porque le ofrezco un ejemplo más intuitivo (y alegre para paliar el desasosiego cerebral).
Tercer ajuste: Ropa mojada
Por la tarde, la misma persona se asoma por la ventana y ve que la ropa tendida está mojándose, este es otro dato adicional que eleva aún más la probabilidad de lluvia, sobre todo si suponemos que vive en una casa, lo que limita la opción de tener vecinos bromistas por arriba. Quizás, tras cotejar mentalmente esta nueva evidencia con la evidencia histórica de escenarios similares, la probabilidad haya subido hasta un 100%. Pero ¿Qué pasa con la tasa base?
- P(A) es la probabilidad inicial de lluvia en Sevilla en agosto, y no ha cambiado. Para el ejemplo 0.01 (1%).
- P(B|A) es la probabilidad de observar la nueva evidencia B (ropa mojándose) dado que A es cierto (si llueve, para el ejemplo es la única opción). Para el ejemplo 1 (100%).
- P(B) es la probabilidad total de observar B, independientemente de si A ocurre o no (ropa mojándose, sólo posible si llueve, así que la probabilidad es idéntica). Para el ejemplo 0.01 (1%).
- P(A|B) es la probabilidad actualizada de A (lluvia) dado que se ha observado B (ropa mojándose). Haciendo los números, la nueva tasa base es de 100%.
¿Por qué ahora sí? Porque B sólo puede darse si A. No hay otra opción (para nuestro espacio muestral) de que la ropa esté mojándose si no llueve, esto iguala la probabilidad de ambos eventos, algo que no pasaba en el anterior ejemplo. Aquí tenemos la tan manida causalidad (basada en la experiencia), no mera correlación.
Estos ejemplos ilustran cómo las nuevas evidencias van modificando la probabilidad inicial pero sin ignorarla. Combinar lo que ya sabemos con lo que estamos observando es crucial para evitar errores como sobrevalorar o ignorar determinados escenarios en la interpretación de eventos.
Para cerrar el bloque, es importante mencionar que el teorema de Bayes es una herramienta muy útil para el cálculo de probabilidades posteriores pero su extensión a teorema de rango como podría ser la lógica deductiva es muy problemática.
Invirtiendo: ¿Y ahora qué?
Una de las críticas al teorema de Bayes es que, si se es completamente objetivo, la probabilidad previa de cada evento es cero. Al haber infinito número de posibilidades, el cálculo de cada una no puede ser otro que cero. Por ello muchos bayesanos han abogado por el concepto de confianza subjetiva para poder justificar cálculos que intenten explicar la realidad. En la inversión la confianza subjetiva puede ser un obstáculo mayúsculo, en especial para el pequeño inversor ¿Qué confianza puede tener en no perder dinero?
Si no partimos de una probabilidad 0 (recomendable para no coquetear con el nihilismo), la experiencia previa dice que el pequeño inversor no lo tiene difícil si sigue ciertas buenas prácticas. Por otro lado, el análisis de las limitaciones inherentes al enfoque probabilístico dice que el pequeño inversor tampoco lo tiene fácil, y esa será seguramente la única conclusión que pueda extraer. Puede que el término conclusión no pasase una revisión mínimamente crítica al tratarse más bien de una obviedad, pero en ella reside una lección fundamental: la probabilidad es una guía, no una garantía. Aunque puede iluminar ciertos caminos, no elimina la incertidumbre ni asegura el éxito. El pequeño inversor debe navegar entre la confianza que brindan los números y la humildad de reconocer que siempre puede haber factores impredecibles que escapan a cualquier modelo probabilístico. Y sí, hacer caso al viejo adagio de «correlación no indica causalidad».
Cuando se dice que la renta variable a largo plazo devuelve un resultado positivo X, uno puede pensar en que la Primera Guerra Mundial fue para muchos, durante los primeros meses de conflicto, «la guerra que acabaría con todas las guerras». Quizás hasta tuviese cierto sentido probabilísticamente, como muchas otras cosas que acabaron no siendo ciertas. Otras, en cambio, eran incluso probabilísticamente imposibles, como que un activo digital sin garantía de ningún tipo hiciese millonarias a no pocas personas. Dependiendo de qué nos pregunten se podría decir que hasta cierto punto todo depende de la experiencia, pero en algunos casos se podría decir que nada dependerá de la experiencia previa, sino de la imposibilidad de conocer el futuro. ¿Entonces qué puede hacer uno para que la inflación no le coma los ahorros?
Puede asignar confianza a lo que dicen los estudios, y buscar flaquezas en tal asignación, aquí se le han presentado algunas herramientas. El espacio muestral es una de ellas, a la hora de definir en qué proceso se tiene más confianza, lo recomendable es al menos considerar un espacio lo suficientemente variado ¿Hay vida más allá de las carteras populares del momento? Si la probabilidad de que indexarse sea la mejor opción es alta puede preguntarse ¿Cuál es la probabilidad de que yo soporte la volatilidad? No olvide fijarse en el espacio muestral de su comportamiento, de poco sirve elegir al «caballo ganador» si no llega a meta montado, puede observarlo si se acerca al hipódromo, en ese caso ganará el siguiente que llegue a meta a lomos de su corcel, por lento que este sea.
También puede recordar el tamaño muestral, esto puede que no le haga ser el más popular de las redes sociales, donde se prodiga reducir el tamaño de la muestra lo máximo posible para que confirme un relato sesgado. «Tal fondo ha sido el mejor de los últimos años» ¿Y cuántos años son esos? ¿Qué pasó los otros años? Son preguntas que incomodarán a algunos, pero ayudan a asignar probabilidades.
Además es posible aplicar ambos conceptos al tiempo de una vida. Si uno escucha a los mayores es probable que oiga con asiduidad “si hubieras vivido lo que yo…”. Hay gente que ha encontrado tréboles de cuatro hojas, visto monedas aterrizar de canto y torres más altas caer, es importante prestar atención a sus vivencias, pues mejoran el cálculo de probabilidades ante lo que se podría definir sólo en base a la experiencia propia. Muchas ramas de la ciencia se fundamentan en ello. Esa conclusión también es obvia, pero no por ello deja de ser un buen consejo.
Si es de aquellos que se atreverían a reservar con muchísima antelación una noche de hotel para el 28 de julio de 2061, lejos de las luces urbanas, con el propósito de presenciar la próxima aparición del cometa Halley, usted confía en las probabilidades calculadas en base a la experiencia de otros y tiene medio camino hecho. El otro medio es exigir un grado de confianza similar a las predicciones que puedan hacerse en campos no tan científicos, como la bolsa o conocerse a uno mismo.
PS: El primer avistamiento del cometa Halley documentado data del año 240 a.c., no quiero decir con ello que tenga que exigir unos 2200 años más de recorrido a la renta variable para poder invertir.




